4.1 Mutliple Correspondence Analysis (MCA)
4.1.1 Definition
Multiple Correspondence Analysis is a dimension reducing method which takes multiple categorical variables and seeks to identify associations between levels of those variables. MCA aims at highlighting features that separate classes of individuals, while determining links between variables and categories. To that end, MCA keeps the core information by the means of principal components which are projected axes (Scholler 2021a).
4.1.2 Complete disjunctive table
MCA can be applied on data stored in a complete disjunctive table which is an indicator matrix.
Figure 4.1: Complete disjunctive table
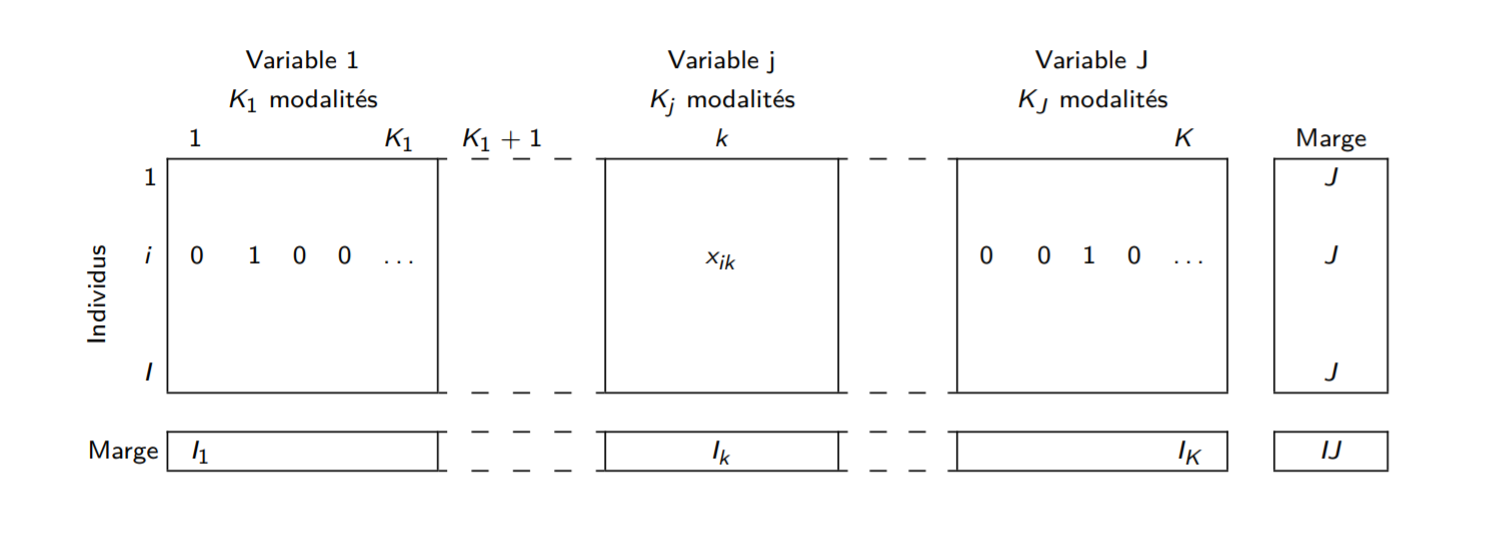
with,
- \(I\) the number of individuals,
- \(J\) the number of variables,
- \(K_j\) the number of categories in the \(j^{th}\) variable,
- \(I_k\) the number of individuals with the \(k^{th}\) category.
4.1.3 Distances
The individuals’ analysis processed by MCA relies on the distance between individuals which is computed as follows for 2 data points \(i\) and \(l\):
\[\begin{equation} d^2(i;l) = \frac{1}{J}\sum_{k=1}^K \frac{I}{I_k}(x_{ik} - x_{lk})^2 \tag{4.1} \end{equation}\]
The distance between two categories \(j\) and \(k\) allows to determine how close they are and is calculated as follows:
\[\begin{equation} d^2(j;k) = \frac{I}{I_k I_j}\times I_{k\neq j} \tag{4.2} \end{equation}\]
with \(I_{k\neq j}\) the number of individuals with one and only one of the \(j\) or \(k\) categories.
4.1.4 Algorithm
- The axes’ origin is placed at the individuals point cloud’s barycenter;
- A sequence of orthogonal axes is seeked so as to maximize the data’s projected inertia;
- These orthogonal projections are represented onto a plan made up of principal components, \((F_1, F_2)\) being the first projected plan.