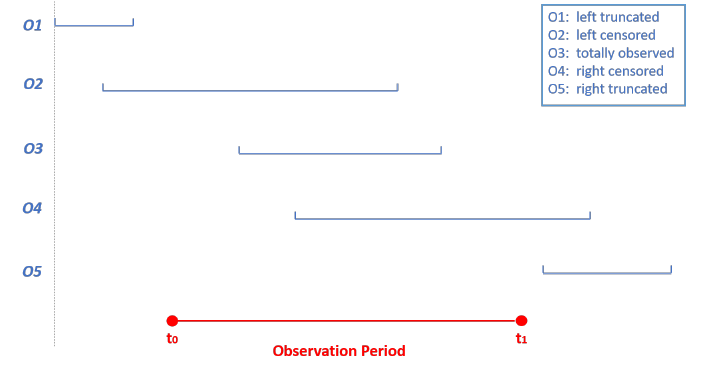
3.2 Censoring and Truncation
When dealing with survival data, some observations are usually censored meaning they are related to spells which are not completely observed. Duration data can also suffer from a selection bias which is called truncation.
3.2.1 Censoring mechanisms
Left-censoring occurs when the event of interest occurs before the beginning of the observation period. For example, an individual is included in a study of unemployment duration at \(t_0\). At that time he has already been unemployed for a period but he cannot recall exactly the duration of this period. If we observe that he finds a job again at \(t_1\), we can only deduce that the duration of unemployment is bigger than \(t_1-t_0\), this individual is consequently left-censored. Observation 2 on figure 3.1 is associated with a left-censored spell (Liu 2019).
A spell is considered right-censored when it is observed from time \(t_0\) until a censoring time \(t_c\) as illustrated by observation 4 on figure 3.1. For instance, the lifetime related to a customer who has not churned at the end of the observation period is right-censored. Let us note \(X_i\) the duration of a complete spell and \(C_i\) the duration of a right-censored spell. We also note \(T_i\) the duration actually observed and \(\delta_i\) the censoring indicator such that \(\delta_i = 1\) if the spell is censored. Then \((t_1, \delta_1),\dots,(t_N, \delta_N)\) are the realizations of the following random variables:
\[\begin{equation} \begin{aligned} T_i & = \min(X_i, C_i) \\ \delta_i & = \pmb{1}_{X_i > C_i} \end{aligned} \tag{3.1} \end{equation}\]
3.2.2 Selection bias
Survival data suffers from a selection bias (or truncation) when only a sub-sample of the population of interest is studied. A customer entering the firm’s portfolio after the end of the study is said to be right-truncated, whereas a client who has left the portfolio before the beginning of the study is considered left-truncated. Mathematically, a random variable \(X\) is truncated by a subset \(A \in \mathbb{R}^+\) if instead of \(\Omega(X)\), we solely observe \(\Omega(X)\bigcap A\). On figure 3.1, the first and fifth observations suffers from a selection bias.
Figure 3.1: Censored and truncated data