3.5 Parametric models

The nonparametric estimation is undoubtedly useful when it comes to have a general overview on the survival data. However, one may want to model the hazard and survivor functions with a functional form in which unknown parameters need to be optimized.

Parametric estimation has a twofold purpose that is to implement a robust model to estimate the risk that a specific event occurs while identifying the variables (or covariates) which best explain this risk.

When implementing parametric models, $\lambda$, $S$ and $\Lambda$ are expressed based on the chosen parametric form. The instantaneous hazard function can either be constant or monotone.

In our study we assume that the explanatory variables are time-constant as we do not have dynamic data at our disposal. Thus, solely time-invariant duration models are presented.

3.5.1 Constant hazard (exponential model)

The exponential distribution models the time between events in a Poisson process and has the key property of being memoryless. Let us note $T$ a time-to-event variable such that $T \sim \mathcal{E}(\theta)$ where $\theta$ is the rate parameter. In this context, memorylessness can be defined as follows:

\[\begin{equation} \mathbb{P}(T>t+s | T > t) = \mathbb{P}(T>s) \tag{3.12} \end{equation}\]

$\forall t \geq 0\ ,\ \theta > 0$ the density, hazard and survival functions can be expressed as:

\[\begin{equation} \begin{aligned} f_{\theta}(t) & = \theta e^{-\theta t} \\\\ \lambda_{\theta}(t) & = \theta \\\\ S_{\theta}(t) & = e^{-\theta t} \\\\ \end{aligned} \tag{3.13} \end{equation}\]

Thus, the exponential distribution is characterized by a constant hazard function which is a consequence of the memorylessness property.

3.5.2 Monotone hazard

Weibull model

The Weibull distribution is a less restrictive generalization of the exponential distribution defined by a shape parameter $\nu$ and a scale parameter $\theta$.

$\forall t \geq 0$ and $\nu,\ \theta > 0$ the density, hazard and survival functions can be expressed as:

\[\begin{equation} \begin{aligned} \lambda_{\nu,\theta}(t) & = \nu \bigg(\frac{1}{\theta}\bigg)^{\nu} t^{\nu - 1} \\\\ S_{\nu, \theta}(t) & = \exp \Bigg( -\bigg(\frac{1}{\theta}\bigg)^{\nu} t\Bigg) \end{aligned} \tag{3.14} \end{equation}\]

The instantaneous hazard function $\lambda_{\nu,\theta}$ is monotonic decreasing if $\nu \in [0, 1]$. For instance, the attrition risk may decrease as the customer’s duration in the portfolio increases. In this context, the client gets more and more loyal to the firm. If $\nu=1$, the hazard rate is constant and $T \sim \mathcal{E}(\theta)$. Converlsely, the hazard function is monotonic increasing if $\nu > 1$. This can be the case when customers tend to continuously search for information on the firm’s competitors, thus becoming more likely to churn as time goes by.

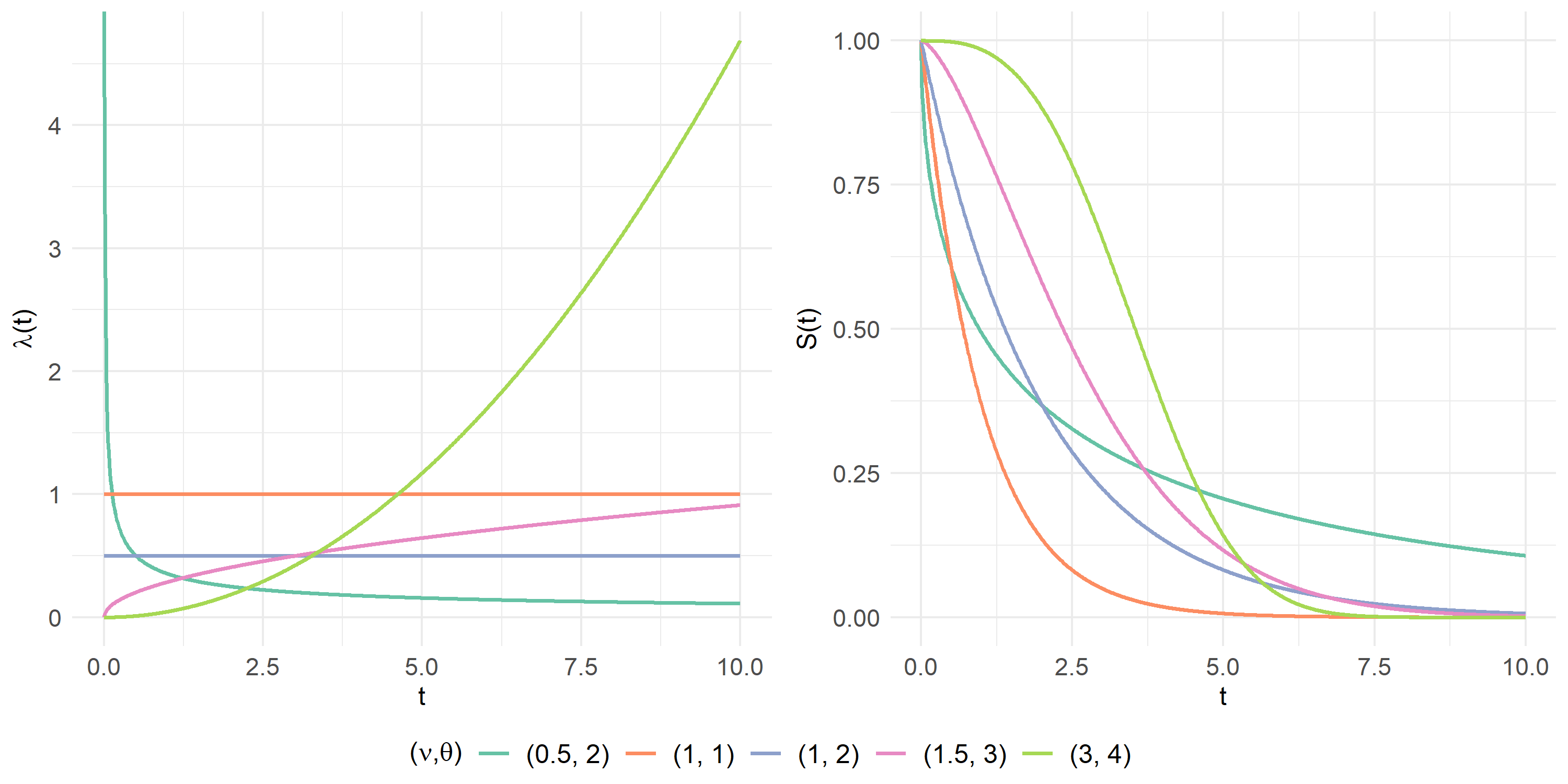
Figure 3.4 illustrates the hazard and survivor functions associated to a Weibull-distributed variable $T$. The two curves’ shape depend both on the shape ($\nu$) and scale ($\theta$) parameters. Some remarks can be made looking at the two plots. When $\nu < 1$ the hazard function is decreasing meaning that the risk of the event occurring decreases as time goes by. When $\nu > 1$ the hazard function is convex increasing which indicates that a marginal increase in time leads to an increase of over one unit in the the hazard function. The higher the shape parameter, the more increasing the hazard function. When $\nu = \theta = 1$, it can be noted that the Weibull distribution corresponds to the exponential distribution (see figures 3.2 and 3.3).

Figure 3.4: Hazard and Survival functions with $T \sim \mathcal{W} (\nu, \theta)$

$Hazard and Survival functions with $T \sim \mathcal{W} (\nu, \theta)$$

Other models

Different probabilistic distributions can be chosen to model the hazard and survival functions related to a time-to-event variable with monotone hazard. The Gompertz model is usually used for mortality data in biostatistics. As for the gamma model, it depends both on the gamma and inverse-gamma distributions and is also based on shape and scale parameters.

3.5.3 Concave and convex hazard

When the hazard function does not evolve in a monotonic fashion, the distributions introduced above are limited. The generalized Weibull model appears to be a good choice to estimate phenomena with concave or convex hazards. It is based on three parameters: $\nu$ (shape), $\theta$ (scale) and $\gamma$. When $\gamma = 1$, the generalized Weibull becomes the Weibull distribution $\mathcal{W}(\nu, \theta)$.