3.3 Probabilistic concepts
In survival analysis, the response variable denoted \(T\) is a time-to-event variable. Instead of estimating the expected failure time, survival models estimate the survival and hazard rate functions which depend on the realization of \(T\).
3.3.1 Survival function
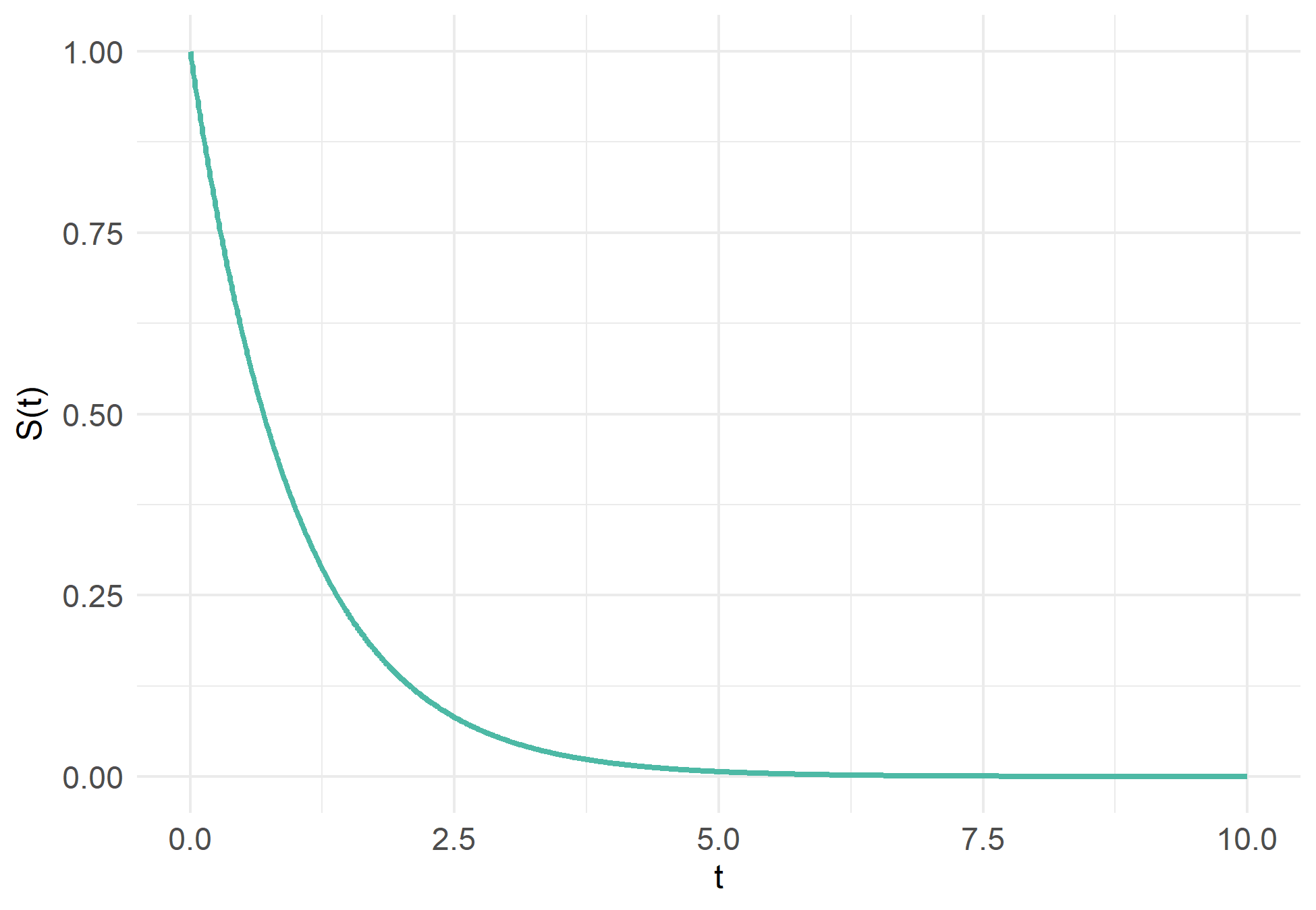
The survival function \(S(t)\) represents the probability that the considered event occurs after time \(t\). For instance, \(S(t)\) can measure the probability that a given customer survives in the portfolio at least until time \(t\). Mathematically, the survival function is defined as: \[\begin{equation} S(t) = P(T > t) = 1 - F(t) \tag{3.2} \end{equation}\]
where \(F(t)\) is the cumulative distribution function.
Figure 3.2: Survival function \(S_T(t)\) with \(T \sim \mathcal{E} (1)\)
3.3.2 Hazard and Cumulative Hazard functions
Another key concept in duration analysis is the hazard function \(\lambda(t)\) which approximates the probability that the event occurs at time \(t\). For instance, \(\lambda(t)\) can measure the probability that a given individual leaves the firm portfolio at time \(t\). Formally, it is expressed as follows: \[\begin{equation} \lambda(t) = \lim_{\Delta t \to 0} \frac{P\big[t \leq T < t + \Delta t | T \geq t \big]}{\Delta t} \tag{3.3} \end{equation}\]
Using the Bayes formula, equation (3.3) can also be written as (see proof (6.3) in the appendix): \[\begin{equation} \lambda(t) = \frac{-\text{d} \ln \big(S(t)\big)}{\text{d} t} \tag{3.4} \end{equation}\]
Finally, integrating the instantaneous hazard function gives the cumulative hazard function which can be more precisely estimated than the hazard function (Cameron and Trivedi 2005) and is defined as:
\[\begin{equation} \Lambda (t) = \int_{0}^{t} \lambda(s) \text{d}s = - \ln \big(S(t)\big) \tag{3.5} \end{equation}\]
Figure 3.3: Cumulative Hazard function \(\Lambda_T(t)\) with \(T \sim \mathcal{E} (1)\)
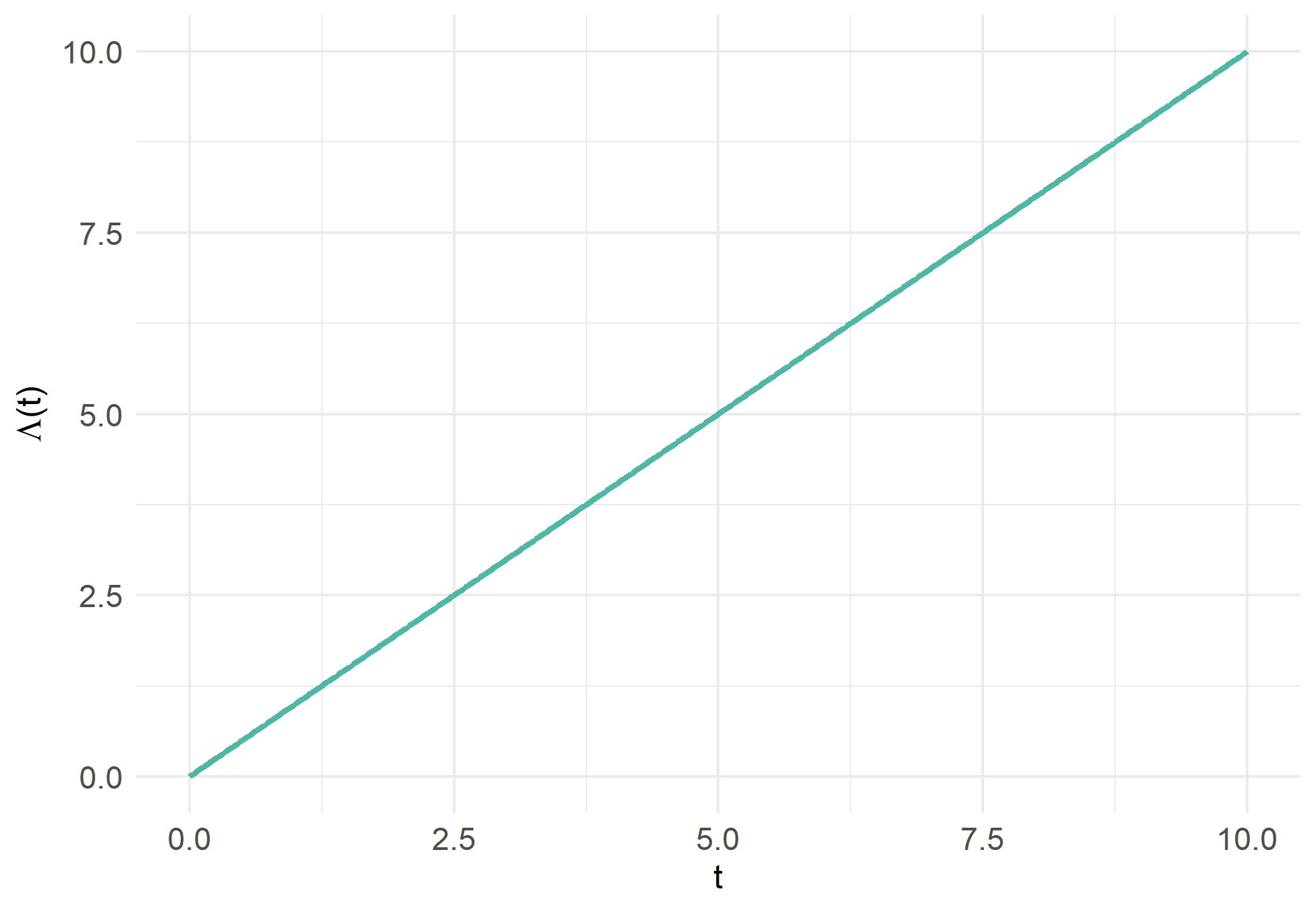
Thus, the hazard, survival and cumulative hazard functions are three mathematical functions which describe the same distribution.